Category: Science

Science, usually research I have done or topics on which I have lectured

Dec 19 2010

What’s on the end of the stick?

gt;

StrafiOnce again I return to science. Lately I’ve been playing with some calculations of the diffusion of one thing into another. This is for work – can’t say what, it’s top secret ;-) I have to admit I’ve rather enjoyed it.

Diffusion calculations ultimately amount to an accounting exercise: this is true of much of physics. You have a bunch of stuff of some sort, and you want to calculate where your stuff will be at some time in the future. The stuff may be electric fields, magnetic fields, heat, molecules or atoms but the point is that new stuff can only be created or destroyed following simple rules and stuff will only travel from one place to another according to other simple rules. Largely it’s a problem of conservation – the amount of stuff is conserved, if stuff leaves one place it must turn up somewhere else.

For diffusion the stuff is molecules, for the purposes of these particular calculations the stuff is not created or destroyed. In the crudest case diffusion is just driven by different amounts of stuff in different places, this is enough to drive the redistribution of stuff since at the molecular level everything is jiggling around at random. If you start with more stuff in one place than another and jiggle it all around at random ultimately it ends up uniformly distributed.

Things can get a bit more complicated, for example you might be interested in your stuff moving into a different environment where it’s not so happy to be or your stuff might be reactive but this is just a smallish change in the basic rules. You also need to define an appropriate boundary condition – what your stuff was doing at one instant in time.

The rules and boundary conditions are expressed as a set of equations; these may have an analytical solution – that’s to say you can write down a further equation that specifies where everything is and when (which you can make into a pretty picture for the boss). Or you may have to carry out a numerical solution: divide time and space up into little pieces and apply the rules in small steps – this is an inelegant but frequently necessary method which, if done naively, can bite you on the arse. Or more technically: “exhibit undesirable numerical instability”.

It turns out that the analytical solution for my current problem can be found in Crank’s “Mathematics of Diffusion”, and so the main work was in making a story for those less interested in equations. The fundamental rules for diffusion are elegant and beautiful, the solutions for specific cases can be ugly and a bit hairy. This is where my skill comes in, to be honest I’m not that good at maths so I couldn’t solve the equations myself – but given a bit of time I can work out which equation is the solution to my problem and carry out calculations with it.

My original adventures with diffusion started in the mid-nineties whilst I was a postdoctoral researcher at the physics department in Cambridge – I was funded by Nestle to measure water diffusing into starch. They were interested in this because at the time they were making a KitKat icecream, which involved putting damp icecream next to crispy wafer with the entirely predictable outcome: the wafer went soggy even when the icecream was stored at –20oC. I spent 18 months or so doing experiments and calculations to demonstrate the very obvious which was if you want to stop your crispy wafer going soggy the best thing to do is coat it in something lardy and therefore water-repellent – chocolate is good! In the meantime I learnt a wide range of things about diffusion and experiments.

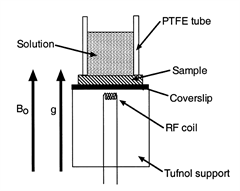
Water diffusing into starch turns out to be a more involved case from a modelling point of view because of the whole “going soggy” thing: basically the properties of the starch change with their water content so there’s feedback between how much water there is and how easy it is for more water to arrive. I did experiments to see where the water was in the starch. This was done using stray-field nuclear magnetic resonance imaging (STRAFI), which required the sample to be stuck on the end of a stick and shoved up the bore of a big magnet, hence the title of this post.

This is another illustration of scientific impact: the core results I relied on for my couple of weeks of calculation date back decades or even hundreds of years. The rules for diffusion were first formulated by Fick in 1855, and since then work has been on-going in solving the equations for ever more complex situations. The 18 months I spent 15 years ago meant that when I returned to it rather then spending several months getting acquainted I could drop pretty much straight in and get some useful results within a couple of weeks. It’s difficult to say what the financial impact for my company might be, with any luck it will save some people at the lab bench a bit of time because results that, are on the face of it, a little odd will have a clear explanation or it may turn out that the calculations show they should stop what they’re doing now because it will never work.

References

  1. Hopkinson, I., R. A. L. Jones, P. J. McDonald, B. Newling, A. Lecat, and S. Livings. “Water ingress into starch and sucrose : starch systems.” POLYMER 42, no. 11 (May 2001): 4947-4956.
  2. Hopkinson, I., R. A. L. Jones, S. Black, D. M. Lane, and P. J. McDonald. “Fickian and Case II diffusion of water into amylose: a stray field NMR study.” CARBOHYDRATE POLYMERS 34, no. 1 (December 5, 1997): 39-47.
  3. Crank, J. “The Mathematics of Diffusion” Oxford Science Publications.

Dec 12 2010

Nevil Maskelyne and Maiden-pap

 

SchehallionOSThis post is about Nevil Maskelyne and his 1775 measurements of the Scottish mountain, Schiehallion (know locally at the time as Maiden-pap), made in order to determine the mass of the earth. My interest in this was stimulated by the Gotthard Base Tunnel breakthrough, since the precision of drilling seemed pretty impressive (8cm horizontal, 1cm vertical see here). There’s a technical explanation of the surveying here. You may wonder how these two things are related.

It’s all about gravity: gravity is the force exerted by one object on another by virtue of their masses. The force is proportional to the masses of the two objects multiplied together divided by the distance between the centres of the two objects squared. This is Isaac Newton’s great insight, although he only applied it to the orbits of celestial bodies. The mass of an object depends on both its density and its volume.

Maskelyne measured the mass of Schiehallion by looking at the deviation of a plumb line from vertical. The problem for the Gotthard Tunnel is that, if you’re surveying underground, measuring the vertical could be hard because if the density of the rocks around you is different in different directions then a plumb-line will deviate from vertical. Actually it’s probably not a huge problem for the Gotthard Base Tunnel, the deviations Maskelyne measured were equivalent to about 1cm over the 14km length of the Gotthard Base Tunnel sections. Furthermore Maskelyne was looking at an isolated mountain: density of about 2500kgm-3 surrounded by air: density about 1kgm-3, under the Alps the variations in density will be far smaller. So we can relax – density variations probably won’t be an important effect. Although it’s interesting to note that the refraction of light by air is significant in the Gotthard Tunnel survey.

Oddly, Newton didn’t consider Maskelyne’s measurements possible, thinking that the force of gravity was insignificant for objects more mundane than worlds. However he demonstrated that for a largish mountain (3 miles high and 6 miles wide) there would be a deviation of the plumb line from vertical of “2 arc minutes”. Angles are measured in degrees (symbol:o) – there are 360o in a circle. Conventionally, if we wish to refer to fractions of a degree we talk about “minutes of arc”, there are 60 minutes in a degree; or even “seconds of arc” – there are 60 seconds of arc in 1 minute of arc. 1 second of arc is therefore 1/1,129,600th of a circle. At the time of Newton’s writing (1687) this deviation of 2 minutes of arc would have been measurable.

Why is measuring the mass of a mountain a job for the Astronomer Royal, as Nevil Maskelyne was at the time? Measuring how much a plumb line is deflected from the vertical is not simple because normally when we want to find vertical we use a plumb line (crudely a string with a weight at the end). The route out of this problem is to use the stars as a background against which to measure vertical. Maskelyne’s scheme was as follows:

  1. Find a mountain which stands isolated from it’s neighbours, with a ridge line which runs East-West and is relatively narrow in the North-South direction. This layout makes experiments and their analysis as simple as possible.
  2. Measure the deviation of a plumb line against a starry background at two points: one to the north of the ridgeline and one to the south (the plumb line will deviate in opposite directions at these two locations).
  3. Carefully survey the whole area, including the location of the the two points where you measured the plumb line and the size and shape of the mountain.
  4. Calculate the mass of the mountain from the survey of its size and shape (which gives you it’s volume) and the density of the rocks you find on the surface.
  5. From the mass of the mountain and the deviation of the plumb line you can work out the density, and therefore mass, of the earth

Measuring the location of stars to the required accuracy is a tricky business since they appear to move as the earth turns and the precision of the required measurement is pretty high. I worked out that using the 3m zenith sector (aka “telescope designed to point straight up”) the difference in pointing direction is about 0.1mm for the two stations – this was measured using a micrometer – essentially a a fine-threaded screw where main turns of the thread only add up to a small amount of progress. The ground survey doesn’t have such stringent requirements, although rather more time was spent on this survey than the stellar measurements.

Reading the 1775 paper that Maskelyne wrote is illuminating: at one point he lists the various gentleman who have visited him at his work! The work was paid for by George III who had provided money to the Royal Society for Maskelyne to measure the “transit of Venus”, some cash was left over from this exercise and the king approved it’s use for weighing the earth.

The value for the density of the earth that Maskelyne measured 235 years ago is about 20% less than the currently accepted value – not bad at all!

References

  1. The wikipedia article is good, including history and physics of the measurements (equations for those that want): http://en.wikipedia.org/wiki/Schiehallion_experiment
  2. This presentation to the Royal Philosophical Society in Glasgow in 1990 has a lot of historical background: http://www.sillittopages.co.uk/schie/schie90.html
  3. Maskelyne’s initial paper “An account of observations made on the mountain Schehallien for finding its attraction” Phil. Trans., 1775, 65, 500-542 is surprisingly readable, and provides details of the experimental measurements. The final analysis of the data was published later.
  4. Map of Schiehallion on Bing (OS mode): http://bit.ly/g1tufF

Nov 29 2010

Book review: Trilobites! by Richard Fortey

Triarthus_lateral
Triarthrus eatoni from Beechers Trilobite bed

This week I’m reporting on “Trilobite! Eye witness to evolution” by Richard Fortey, which I came to via Attenborough’s “First Life” TV programme and advice from @crafthole. As usual this is intended as part notes for my own edification and part review. I read the Kindle version of this book, I’d recommend getting the paper version since the publishers have made no effort to incorporate any of the illustrations from the book into the electronic edition.

Fortey has a rather literary style which makes for rather pleasing reading: the book starts with a walk along the cliffs beyond Boscastle to a location used by Thomas Hardy in “A pair of blue eyes” where the hero comes face to face with a trilobite embedded in the cliffs. The book covers the discovery of trilobite anatomy; evolution, the drifting continents and what makes a palaeontologist tick.

Trilobites were common in the relatively early history of life on earth, during the Cambrian period, about 500 million years ago and became extinct at the end of the Permian period about 250 million years ago. The book starts with a description of trilobite anatomy – you can see the details on the wikipedia page. The basic fossil remnants are the hard shell of the trilobite, the upper surface shield – the closest living relatives to trilobites are things like woodlice and the horseshoe crab (which Fortey eats in Thailand!). Generally legs and soft parts do not fossilise, so it was some time before these structures were understood.

The first written record of a trilobite was by Dr Lhwyd in a letter to Martin Lister, reported to the Royal Society in 1699. It is a fleeting mention, and he mis-identifies his find as a “skeleton of some flat fish”, noting that they are abundant but his illustration is quite clearly of a trilobite. Dr Lhwyd writes from Wales and much of the early history of the trilobite’s discovery is tied up with Wales, trilobites are characteristic of the Cambrian period, named after Wales.

The image at the top of this post illustrates the discovery of trilobite legs. Most trilobites lost their legs in the fossilisation process, they are flimsy and poorly armoured. However in the case of the Beechers’ trilobite bed special preservation circumstances have fossilised the legs, in this case picked out in ‘fools gold’ or iron pyrite.

I was rather impressed by the chapter on trilobite eyes, as reported in my post on First Life, trilobite eyes are made from calcite – an array of calcite hexagonal prisms in the eye channels light to light receptors. Calcite is birefringent, one of the features of this property is that light only travels along the prisms to the light sensors if it enters them square on. So the relatively large number of calcite prisms in trilobite eyes suggest resolution comes from directional selectivity of the prisms. Some trilobite eyes are more complex than this: the Phacops eye is comprised of fewer prisms but with cunning lenses at the outside faces which work using magnesium concentration gradients to eliminate chromatic aberration – this suggests they channel light to multiple light receptors. Calcite is calcium carbonate, but the calcium can be selectively replaced by magnesium which changes it’s optical properties – in terms of man-made optics this type of thing is feasible but it’s pretty sophisticated. Reading this on the train the temptation to grab fellow commuters and jab my finger at the appropriate paragraph shouting “Have you read this about trilobite eyes, it is flippin’ incredible!!” was almost overwhelming!

Fortey is clearly passionate about his topic, as he says of breaking rocks to find the trilobites therein:

“Hardened criminals used to be required to do the same thing before it was banned as inhumane. I loved it.”

He works as a palaeontologists tasked with identifying trilobites, and if necessary creating new species. I learnt that the Linnean binomial system is slightly more complex than I thought, as well as having a two part name each species is tagged with the name of the person who first described a species this helps the expert in the field trace the original citation for a species. You gain the impression of someone able to identify one trilobite of a myriad potential species from mere fragments, in the manner of those archaeologists who can apparently build a pot, complete with its history, from a tiny shard. As arthropods with tough exoskeletons, trilobites moulted their shells to grow – each animal strewing the landscape with potential fossil fragments: fossil factories, Fortey calls them. He goes into some detail of the inferred life styles of trilobites and their development i.e how juveniles grow into adults. For some of the developmental stuff it would be nice to see the supporting fossils: it sounds ferociously difficult separating juvenile forms from different species of trilobite.

The large variety of trilobites, and their appearance in the early days of fossilising life, makes them a useful tool in the study of how evolution operates. Fortey rebuts the proposal by Stephen Jay Gould in “Wonderful Life” for a Cambrian explosion producing massive diversity of forms, beyond what we see now. Arguing from research by former colleagues that the variation in forms discovered in the Burgess Shale is much smaller than Gould claims. The difference being in the interpretation of how diverse forms are from relatively indistinct fossils. This is perhaps a warning to the casual reader that controversies are easily hidden in the popular science literature.

A second application of trilobites is in the dating of rocks: they are very common, fossilise well and, over a period of time, evolved into many distinctive forms which makes them ideal for the purpose. Finally they can also be used in the reconstruction of ancient continents: identifying common collections of trilobites in disparate parts of the world suggests they were originally found in one place.

As mentioned at the top of page, my Kindle edition of this book was bereft of illustrations but by the power of google, I can give you phacops, famous for it’s fancy eyes, ollenelus – one of the commonest of the early trilobites, calymene blumenbachii pleasingly convex as Fortey says, paradoxides another early species, Ogygiocarella debuchii as discovered by Dr Lhywd.

I found this book most useful as an insight into the mind of a palaeontologist and a taxonomist.

Further reading
An overview of trilobites
A piece by Fortey in American Scientist on trilobites (pdf)

Nov 16 2010

First Life

Charnia, Image by Leicester Museum

The latest, and perhaps last, David Attenborough TV series is the two episode First Life: about the very earliest life on earth. It ends as the first life emerges from the sea.

David Attenborough is a hero in our household: Mrs SomeBeans and I saw his “Life on Earth” series at an impressionable age; he is our matchmaker, were it not for “Life on Earth” Mrs SomeBeans would not have gone to university to study zoology, which is where she met me – at university, not as a zoology specimen, I hasten to add! The good thing about a David Attenborough nature programme, is that they are rich enough that even someone who had done a degree in zoology will actually learn quite a lot of stuff. Attenborough’s autobiography, Life on Air , is also well worth a read – perhaps the most striking thing is the realisation that someone still alive was involved in creating the TV documentary format.

Returning to “First Life”: the programme starts with Charnia  a fossil identified in Charnwood Forest – close to where Attenborough grew up, it was the first fossil found in Precambrian rocks, dating to at least 580million years ago, which had previously been thought devoid of life. As a time yardstick: the earth is about 4billion years old and the dinosaurs flourished between 230million and 65 million years ago. Charnia looks like a simple frond, it lived in the sea. It is distinct from the later fossils found in the Precambrian and has no modern relatives – in this sense it was a dead-end for life.

Following the Charnwood Forest fossils (examples of which are found around the world) the program turns to two further earlier fossil collections at Mistaken Point in Canada and in the Ediacara Hills in Australia. These data from a slightly later period. The Ediacara fossils were the first such collection of fossils found, whilst those at Mistaken Point are the most diverse. As fossils they are fairly subtle marks in the rocks, the creatures from which they derived were soft-bodied – it’s surprising the range of conclusions the experts come to on such markings: inferring early reproduction and feeding strategies.

The second episode focussed largely on the fossils found in the Burgess Shale, in the Canadian Rockies, I’ve written about them previously. The key point is that the Burgess Shale assemblage dating to about 500million years ago, exhibits an enormous range of forms – more diverse than seen now, many of which have subsequently become extinct. The fossilisation conditions of the Burgess Shale mean that the soft parts, rather than just the hard parts of the animals are preserved. Seeing them on film there are several striking things: the Burgess Shale quarry is tiny, perched half way up a steep scree slope and the fossils are smaller than I had thought most only two or three centimetres long and very subtle – thin film like fossils only visible in the rock from certain angles.

In contrast the fossil trilobites from the Atlas Mountains in Morocco were outright awesome (not a word I use often or lightly). They’re beautifully detailed, and in full 3D including all manner of weird, delicate bristles and appendages Stacks of pictures of the trilobites can be found using the appropriate Google Search. That looks a bit of a dry description, they really are flippin’ fantastic fossils. I’d never realised such fossils existed! The fossil below is from a species which became extinct 400 million years ago – the trilobites became extinct 250 million years ago.

Trilobite: Walliserops Trifurcatus (Image from FossilMall)

Apparently the eyes of the trilobite are made from calcite lenses – unlike any modern animal. This is interesting because calcite is birefringent so the eyes could potentially have given trilobites polarisation sensitive vision. It implies a high degree of control of the crystallisation of the mineral. Along with the trilobites, sizeable sea scorpions (eurypterid) were found – some up to 2.5metres in length (see here) – this is 1950’s b-movie sized arthropod!

First Life is a nice little series about something deeply interesting: how the very first life looked and is nicely executed with location work, expert contributions from real experts and computer graphics visualisations of the living creatures derived from the often badly squashed and indistinct fossils. I wish it had been longer! Thanks to a fellow tweep I have put Richard Fortey’s “Trilobite: Eye Witness to Evolution” on my reading list.

Nov 03 2010

Book review: The Scientific Revolution and the Origins of Modern Science by John Henry

ScientificRevolution_JohnHenryThe book I review in this post is “The Scientific Revolution and the Origins of Modern Science” by John Henry. In contrast to previous history books I have read this is neither popular history of science, nor original material but instead an academic text book. My first impressions are that it is a slim volume (100 pages) and contains no pictures! Since childhood I have tended towards the weightier volume, feeling it better value for money.

The Scientific Revolution is a period in European history during which the way in which science was done changed dramatically. The main action took place during the 17th century with lesser changes occurring in the 15th and 18th centuries. The Royal Society, on which I have blogged several times, plays a part in this Revolution and God’s Philosophers by James Hannam is one view of the preamble to the period.

The book starts with a brief introduction to historiography (methods of history research) of the Scientific Revolution, with a particular warning against “whiggish” behaviour: that’s to say looking back into the past and extracting from it that thread that leads to the future, ignoring all other things – the preferred alternative being to look at a period as a whole in its own terms. History as introduced by scientists is often highly whiggish.

Next up is a highlighting of the Renaissance, a period immediately prior to the Scientific Revolution wherein much renewed effort was made to learn from the Classics, the importance of the Renaissance appears to have been in initiating a break from the natural philosophy and theology taught in the universities of the time, which were teaching rather than research institutions.

The Scientific Revolution introduced two “methods of science” which differentiated it from the previous studies of natural philosophy: mathematisation and experiment. Mathematisation in that for sciences particularly relating to physics the aim became to develop a mathematical model for the physical behaviour observed. Prior to the Revolution mathematics was seen almost as a menial craft, inferior to both natural philosophy and theology which relied on logical chains of deduction to establish causes. These days mathematics has a far higher prestige, as illustrated in this xkcd comicstrip. The second element of experimentation means the use of controlled experimentation rather than pure thought to determine true facts.

One of the more surprising insights for me was the influence of magic on the developing science, very much in parallel to the influence of alchemy on the developing chemical sciences: magic was a physical equivalent. Magicians were intensely interested in the mysterious properties of physical objects and were early users of lenses and mirrors. The experience they developed in manipulating physical objects was the equivalent of the experience the alchemists gained in manipulating chemicals. Some of this thinking went forward into the new science the remaining rump of bonkers stuff left behind.

It’s very easy to glibly teach of forces and atoms to students, or perhaps blithely demonstrate the solution to an, on the face of it, tricky integral. However, we take a lot for granted: the great names of the past were at least as intelligent as more recent ones such as Einstein or Maxwell yet they struggled greatly with the idea of a force acting at a distance and so forth and that’s because these ideas are actually not obvious except in retrospect. Mechanical philosophies of Descartes and Hobbes were amongst the competing ideas for a “system of the world” ultimately supplanted by Newton.

Henry highlights that most of the participants in the Scientific Revolution were religiously devout, as were many in that time. An interesting idea taken up, but now apparently rejected, was that Puritanism was essential in driving the Scientific Revolution in Britain. Despite this, it was in this period that atheism started to appear.

A few times Henry refers to differences in emphasis between the developing new science in Britain when compared to the Continent. In Britain the emphasis was on an almost legalistic approach with purportedly bare facts presented to a jury in the form, for example, of the fellows of the Royal Society – theorising was in principle depreciated. This approach originates with Francis Bacon, a former Attorney General and experienced legal figure. On the Continent the emphasis was different, experiments were seen more as a demonstration of the correctness of a theory. The reason for this difference is laid at the door of the English Civil War, only briefly passed when the Royal Society was founded. It is argued that this largely non-confrontational style arose from a need for a bit of peace following the recent turmoil.

In sum I found this book an interesting experience: it’s very dense and heavily referenced. Popular history of science tends to revolve around individual biography and it’s nice to get some context for these lives. I’m particularly interested in following up some of the references to other European learned societies.

Further Reading

The book provides a list of handy links to online resources:

  1. Stanford Encyclopaedia of Philosophy
  2. Prof. Robert A. Hatch’s Scientific Revolution Website
  3. Prof. Paul Halsall’s Scientific Revolution Website
  4. SparkNotes Study Guide on the Scientific Revolution
  5. The Robert Boyle Project
  6. The Galileo Project
  7. The Newton Project
  8. The MacTutor History of Mathematics Archive

These all look interesting, and although not polished I’ve been using the MacTutor for many years.